水族館で出会った最大の疑問
──その後本格的に動物の形の研究に移られたのでしょうか?
近藤 そうですね。本庶先生のもとでの研究がひと段落して、もう免疫は十分やり切ったと感じました。じゃあ次に何をやろうか。やっぱりずっと心に残っていたのは生き物の形でした。だったら、次は遺伝子の仕組みを研究したほうがいいと思ったんです。
例えば、血管の細胞と筋肉の細胞には異なる遺伝子が働いているから、異なる形や働きをしているわけですよね。そこを知るために東京大学医学部の村松正實先生の研究室に入りました。
その研究をしているとき、遊びに行ったサンシャイン水族館で、今後の研究人生を決める大きな出会いをしました。ナポレオンフィッシュの模様です(写真1)。水族館でナポレオンフィッシュを見た時、「こんな複雑な模様、いったいどうやってできるのだろう」と衝撃を受けたのです。もし左右対称なら、遺伝子の中に「模様の地図」があって、こことここに線を引く、というように説明できるかもしれない。でも、ナポレオンフィッシュの模様は全く左右対称ではないのです。

──遺伝子に直接「設計図」があるわけではないのですね。
近藤 そうなんです。そもそも生き物の体の中に、マス目のように番地が振られた「位置情報」があれば、どのマスに何を置くか決めることができます。でも、ただの細胞にどうやってそんな情報が与えられるのか。ここが「生き物の模様づくり」の最大の謎だと思いました。
先ほども少し例に出しましたが、例えば、広場に何百万人も集めて、一人ひとりが色のついたプラカードを掲げて模様をつくる場面を想像してみてください。それができるのは「あなたはこの位置にいるから、この色のプラカードを掲げて」と設計図に基づいて個別の指示があるからです。ただ人を集めて「ストライプをつくれ」と一斉に声をかけても、一人ひとりが全体の設計図を持っているわけでも、自分の位置を知っているわけでもないので模様はできません。でも、生き物の細胞たちは不思議なことに、まるでそれをやってのけているかのように見えるのです。それがなぜ可能なのか、私には不思議でしかたなかった。
この疑問を同じ研究室の人に言って回っていたんですね。そしたら僕より一つ年下の同じ苗字の近藤君が「君の言っていることの答えになるような論文があるよ」と教えてくれたのです。そこにあったのが、チューリング理論に関する記述です。
──あの数学者アラン・チューリング(1912年-54年)でしょうか?
近藤 そうです。暗号解読やコンピュータの基礎で有名な天才数学者です。彼が生涯で唯一、生物について書いた論文があって、そこで提案されたのが「チューリング波」という仕組みでした。”The Chemical Basis of Morphogenesis”(形態形成の化学的基礎)という論文名で1952年に発表しています。
この論文では、体の中で化学反応が干渉し合うことで波が生まれ、その波が細胞に「ここが位置だ」という情報を与える。模様や構造の多くは、この等間隔のパターン、つまり波で説明できると示したんです。
体の中に化学反応の波がある?
──生き物の体に波? 想像がつきません。
近藤 そうですよね。天才しか思いつかない画期的なアイデアです。
チューリングもきっと、動物の体や模様がどうやってできるのか疑問に思ったのでしょう。観察を重ねるうちに、多くの模様や構造には「等間隔の繰り返しのパターン」があると彼は気づいたのです。縞や斑点などが規則的に並んでいる。それを一言で言えば「波」なんですね。
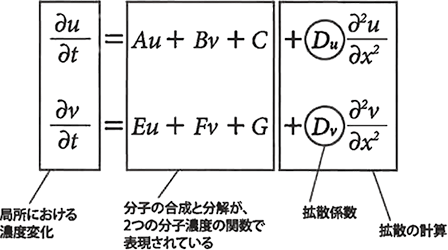
ただ、物理的な波が体の内部にできるというのは、考えにくいです。だから、チューリングは化学反応で波ができる可能性を考えました。体の中で複数の化学反応が互いに干渉し合うと、一定の間隔で波が立ち上がる可能性があることを数学で証明したのです。これを反応拡散原理(チューリング波)と呼びます。その波こそが細胞に「ここが位置だ」という情報を与えて、形や模様をつくる。チューリングはそう考えました。それが数式1です。
──「位置情報をつくる」というのは、細胞のどこに何ができるかを決める仕組み、ということですか?
近藤 そうですね。普通の生物学者では思いつかないような理論でしたが、数学的にきちんと証明されていたのです。
そこで、僕も半信半疑でチューリング理論をプログラムに組んで計算させてみることにしました。すると、位置情報なんて何もないところから、ナポレオンフィッシュそっくりの模様が浮かび上がってきたのです。初めて見たときは、鳥肌が立ちました。
さらに、数式の係数をちょっといじるだけで、今度はキリンの縞やダルメシアンの斑点が出てくる。模様が次々と現れるのを見ながら、「こんなに簡単に説明できちゃうのか」と驚いたのを覚えています。
──つまりナポレオンフィッシュに限らず、多くの模様がチューリング波で説明できる?
近藤 そうなのです。繰り返しの模様ならなんでもつくれるのがチューリング波です。しかも最初に何か情報を与える必要もない。実際に目の前で模様が浮かび上がってくるのを見て、理論のあまりの完璧さにしばらく呆然としてしまいました。ここまで完璧だともう僕がすることは何もないな。答えはすでにここにあると。
でも同時に、「いや、待てよ」とも思った。生き物の模様の原理をここまで完璧にチューリングは説明しているのに、当時は世界で波の存在を信じている人がほぼいなかった。ここが問題です。チューリング波は、彼の死後に、何人かの物理生物学者によって発掘され、一時期盛り上がりましたが、生物学者からすれば「波が体をつくるなんてあり得ない」と一笑に付されるような話だったんです。誰もがこの理論は現実的ではないと考えていました。
でも、僕は「魚の模様はチューリング・パターン以外の何物でもない」と確証していました。そして、その模様の動きを観察するだけで証明になる、と頭の中ではすでに完成していたのです。こうなったら、「東大にいる場合じゃない。生き物の形そのものを研究するべきだ」と考え、スイスのバーゼル大学に移ることにしたんです。
──ご自身の直感に従って行動されたのですね。
近藤 バーゼル大学では、Walter Gehring教授の研究室に入りました。形態形成に関係する遺伝子を研究する研究室で、チューリング波に関する自分の考えがどうなのか確かめたかったという目的もあります。
当時この研究室は、ショウジョウバエで体の設計図を決める「ホメオボックス遺伝子(Hox遺伝子)」を発見したことで、世界的に注目されていた時期でもありました。だからなのか、この研究室でもチューリング波に興味を持つ人は一人もいませんでした。僕のシミュレーションを見せても、「へー」という感じで誰からも相手にされなかったのです。
しかし、僕は自分の説に確信を持っていたので、「この人たちの理解力がないだけだ。むしろ、理解されなければされないほど驚くべき発見であることの証だ」と考えていました(笑)。
魚の模様が動けば世界中を納得させられる
──具体的にどのように生き物の中にある波を実証しようと考えていたのでしょうか?
近藤 チューリング波の重要な性質の一つに、パターンを乱されても周囲の波が動いて、最終的に一定の間隔へ戻ろうとするというものがあります。この性質を生き物に当てはめます。
生き物は成長すると体が大きくなるので、模様の間隔が本来の安定した間隔より広がってしまうんです。しかし、その状態は不安定なので、波が動いて間隔を調整し、また安定な状態に戻ろうとする。これを実際の生き物で観察できれば、チューリング波の存在を証明できると考えました。
問題はどの生き物で試すかです。シミュレーションではナポレオンフィッシュの模様が理想的でしたが、実際に飼育するには大きすぎるし、模様も複雑で変化がわかりにくい。そこで最適なのがタテジマキンチャクダイ(写真2)です。体側に直線的なストライプがあり、そのストライプが枝分かれして動きながらも等間隔を保とうとするなら、まさにチューリング波の実証になる。この構想はスイスにいる時からすでに頭の中ででき上がっていました。
──あとは実験をするのみです。
近藤 そうしたい気持ちは山々でしたが、当時の僕にはこの研究での実績は全くありません。また、チューリング波の存在も誰も信じていなかったので、もちろん研究費なんて出るわけがありませんでした。
ちょうどその頃に本庶先生から「日本に戻ってきて免疫の研究をやらないか」と声をかけてもらっていました。じゃあ昼間は本庶研で仕事をして、夜や休日に自宅でタテジマキンチャクダイを飼って「隠れ実験」をすればいいのだと。本庶先生には絶対にバレちゃいけないから隠れ実験です。本庶研では研究に人生を全部捧げるのが当たり前で、関係ない実験をこそこそやってるなんて絶対許されない世界でしたから。